Introduction
In solid-state physics, the work function (sometimes spelt workfunction, WF) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here “immediately” means that the final electron position is far from the surface on the atomic scale (the force between the electron and its image charge in the surface can be neglected, many nm), but still too close to the solid to be influenced by ambient electric fields in the vacuum. The work function is not a characteristic of a bulk material, but rather a property of the surface of the material (depending on crystal face and contamination).
The work function $W$ for a given surface is defined by the difference
\[W = -e\phi - E_F\]where $−e$ is the charge of an electron, $\phi$ is the electrostatic potential in the vacuum nearby the surface, and $E_F$ is the Fermi level (electrochemical potential of electrons) inside the material. The term $−e\phi$ is the energy of an electron at rest in the vacuum nearby the surface. Because the Fermi level is the chemical potential of the system, by definition, the work function is equal to the energy difference between the Fermi level and the vacuum level at the surface of the material.
In practice, one directly controls $E_F$ by the voltage applied to the material through electrodes, and the work function is generally a fixed characteristic of the surface material. Consequently, this means that when a voltage is applied to a material, the electrostatic potential $\phi$ produced in the vacuum will be somewhat lower than the applied voltage, the difference depending on the work function of the material surface. Rearranging the above equation, one has
\[\phi = V- \frac{W}{e}\]where $V = −E_F/e$ is the voltage of the material (as measured by a voltmeter, through an attached electrode), relative to an electrical ground that is defined as having zero Fermi level. The fact that $\phi$ depends on the material surface means that the space between two dissimilar conductors will have a built-in electric field, when those conductors are in total equilibrium with each other (electrically shorted to each other, and with equal temperatures).
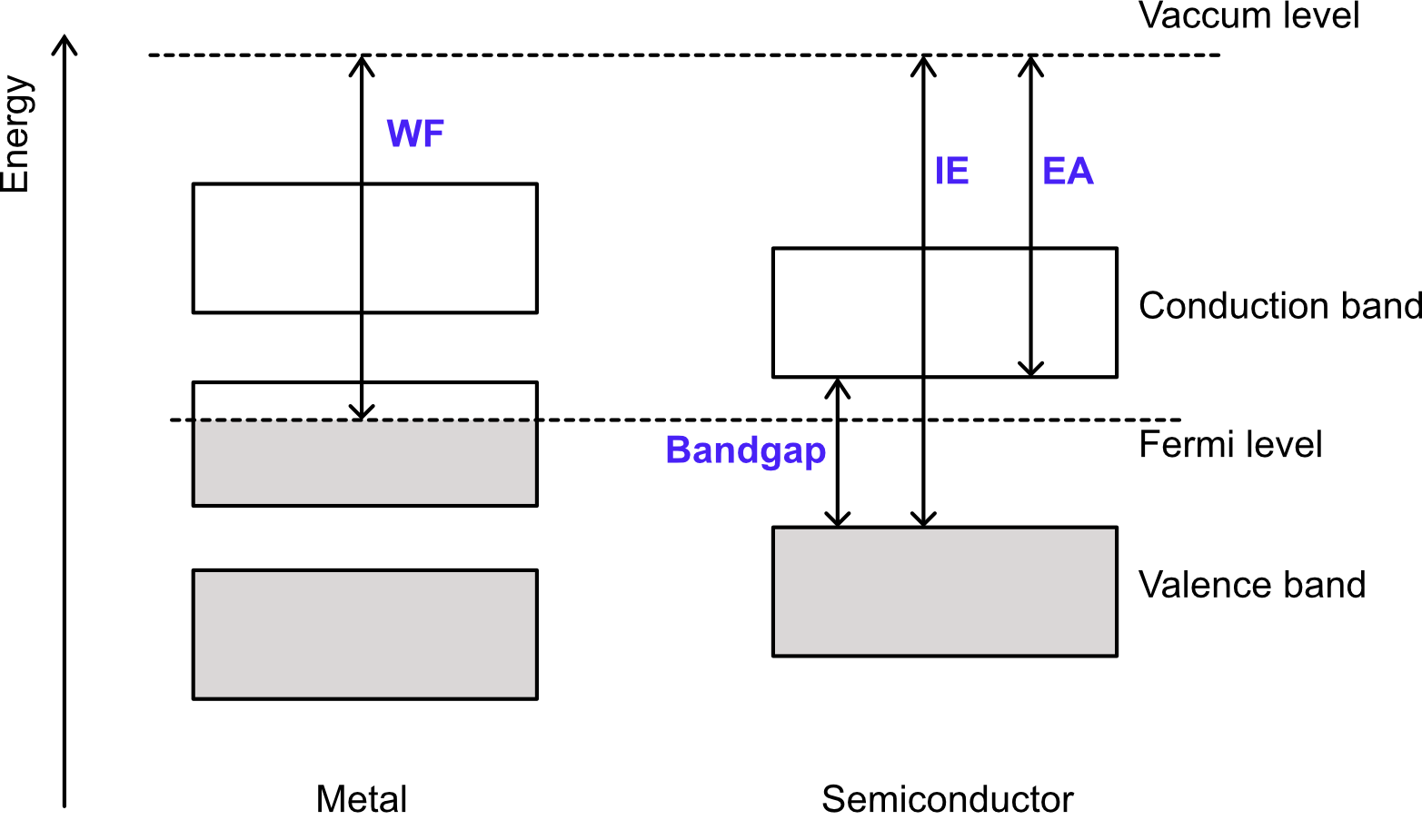
Figure 1. Schematic band diagram for metal and semiconductor
Here, one should note that the minimum energy required to extract one electron from either a semiconductor or insulator is not the WF but the ionization energy (IE). The electron affinity (EA), which is the energy released by adding one electron to a material, is a concept similar to the WF but the direction of electron transfer is opposite. For metals, the EA has the same value as the WF (See Figure 1).
WF of Elements
Because WF is dependent on the cleanliness of the surface, measurements reported in the literature often cover a considerable range. Figure 2 contains selected values for the electron work function of the elements which may be regarded as typical values for a reasonably clean surface. Those values, marked R in the table, come from analysis of results from different measurement methods. The method of measurement is indicated for each value. The following abbreviations appear:
| Abbre. | Full name |
|---|---|
| R – | Recommended value |
| TE – | Thermionic emission |
| PE – | Photoelectric effect |
| FE – | Field emission |
| CPD – | Contact potential difference |
| polycr – | Polycrystalline sample |
| amorp – | Amorphous sample |
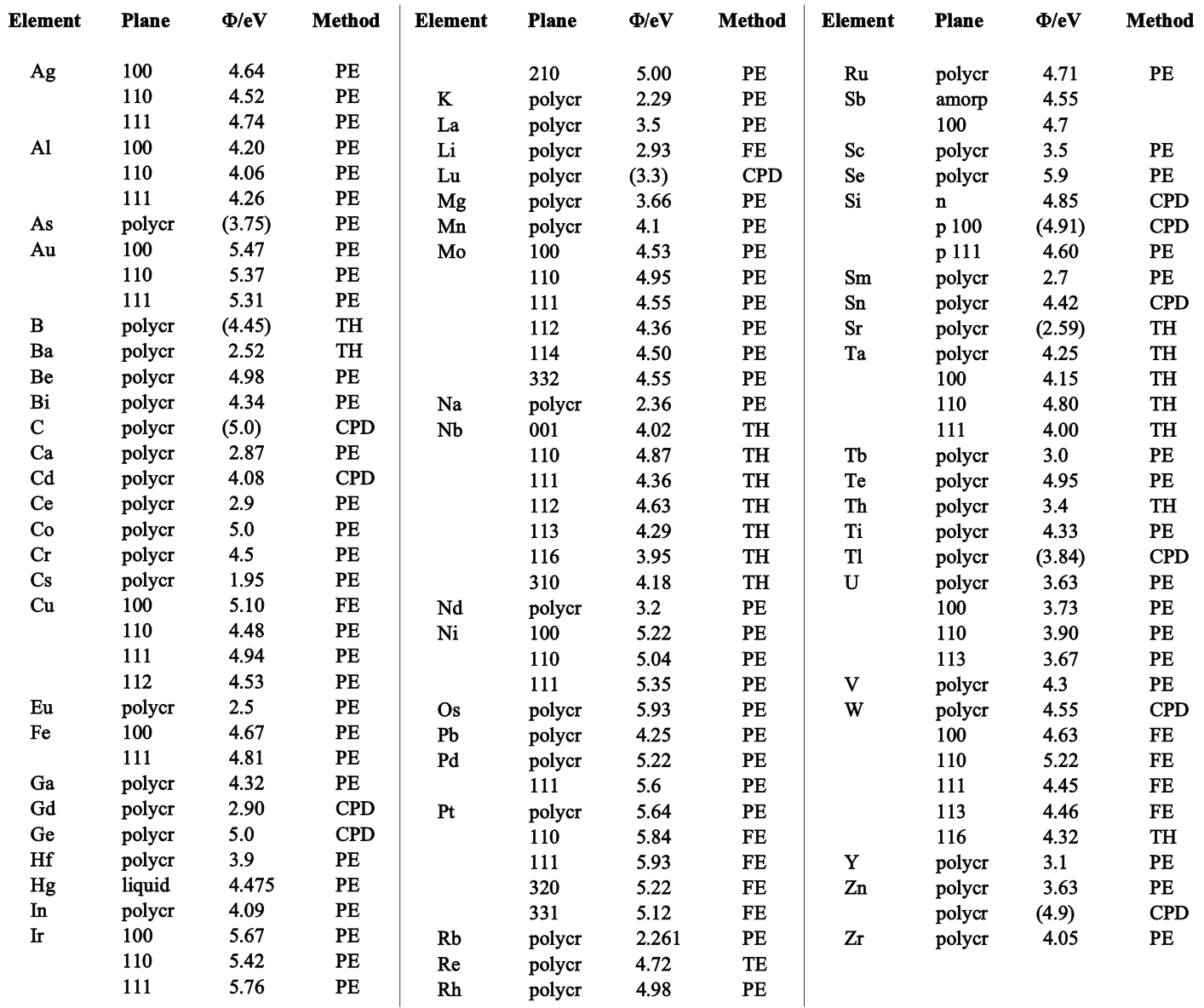
Figure 2. Work function of elements
WF of Metal Oxides
The WFs of metal oxides can be difficult to reproduce because there are so many factors that alter an oxide’s work function (WF values for a given material can span over 1 eV). The large variation in reported WF values is because WF represents the sum of electron chemical potential and surface dipole, and it is very sensitive to a number of factors. Fators such as surface roughness, exposed crystal face, radiation exposure, and adsorbate coverage affect the surface dipole component, whereas electron chemical potential is affected by the chemical identity of a material, the presence of impurities and the stoichiometry of a material.
Although there are many factors that can alter WF, it is possible to gain control over many of these factors to tune WF. Under certain preparation conditions, one can obtain reproducible WF values for a given material. A compilation of WF values for various metal oxides (prepared by in-situ metal oxidation) is provided in Table 1. The values in Table 1 represent the average of the most thermodynamically stable crystal faces of each oxide, as the oxides represented here were polycrystalline and prepared by in-situ metal oxidation. The oxides were not exposed to air, so adsorbates likely have a minimal effect on the WF values shown here. Furthermore, as the oxides were prepared via in-situ oxidation (and vacuum annealing in the case of reduced oxides), they should all consist of stable oxygen-terminated surfaces. Consequently, the magnitude of the surface dipole in the WF values listed in Table 1 can be considered similar in magnitude. Thus, the values allow an approximate comparison of relative electron chemical potential values.
| Oxide | WF (eV) | IE (eV) | Bandgap (eV) | Oxide | WF (eV) | IE (eV) | Bandgap (eV) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TiO$_2$ | 5.4±0.2 | 8.0 | 3.4 | V$_2$O$_5$ | 6.8±0.1 | 9.26 | 2.8 | ||||
| MoO$_3$ | 6.82±0.05 | 9.4 | 3.0 | Cr$_2$O$_3$ | 5.0±0.5 | 6.5 | 3.2 | ||||
| CuO | 5.9±0.1 | 5.7 | 1.4 | CrO$_{3−x}$ | 6.75±0.2 | 9.0 | 2.25 | ||||
| Cu$_2$O | 4.9±0.1 | 5.5 | 2.3 | MoO$_2$ | 5.9±0.2 | 6.0 | 0 | ||||
| NiO | 6.3±0.2 | 6.7 | 3.2 | Ta$_2$O$_5$ | 5.2±0.2 | 8.9 | 3.9 | ||||
| WO$_3$ | 6.8±0.4 | 9.8 | 3.4 | V$_2$O$_3$ | 4.9 | ||||||
| CoO | 4.6±0.2 | 5.2 | 2.4 | W${18}$O${49}$ | 6.4±0.1 | ||||||
| CO$_3$O$_4$ | 6.3±0.3 | 6.4 | 1.6 | TiO | 4.7±0.2 | ||||||
| Ag$_2$O | 5.51 | 6.4 | 1.3 |
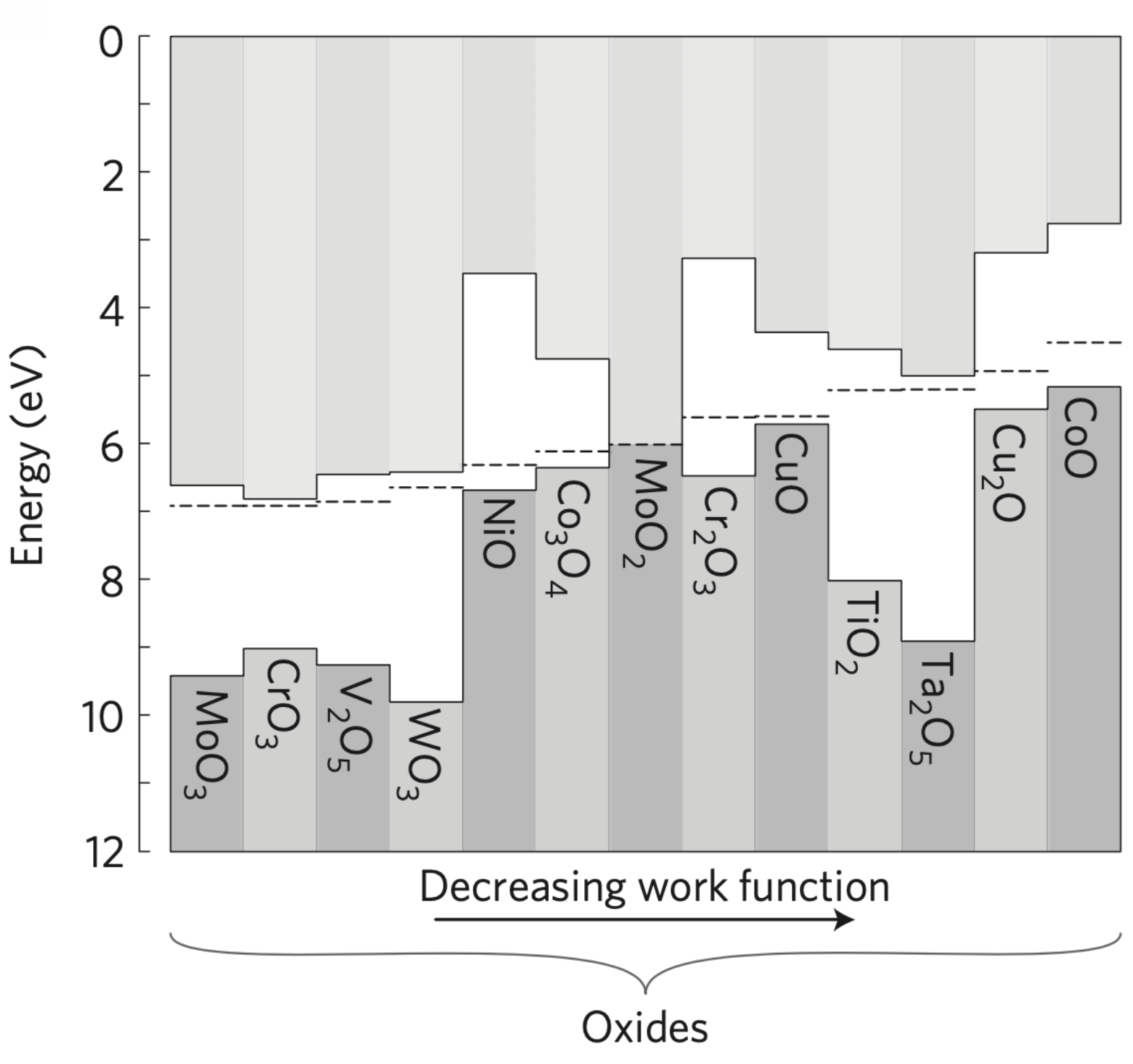
Figure 3. Energy levels of in-situ oxidized metal oxides on an absolute energy scale (determined from direct and inverse photoemission).
- Reducing the cation oxidation state of an oxide tends to decrease its work function
- Removing oxygen in an oxide tends to decrease the work function, whereas adding oxygen tends to increase its work function.
- Work function of an oxide after the air-saturated (approximately a week later in air) is universally lower than the initially measured value with a difference that scales with the initial work function.
WF of Other Common Materials
| Material | WF (eV) |
|---|---|
| ITO | ~4.7 |
| FTO | 4.4 |
| Graphene | ~4.4 |
Reference:
- Wikipedia-work function, https://en.wikipedia.org/wiki/Work_function.
- ELECTRON WORK FUNCTION OF THE ELEMENTS
- Universal energy-level alignment of molecules on metal oxides, Nature materials 2012, 11.1: 76-81.
- Universal Work Function of Metal Oxides Exposed to Air, Advanced Materials Interfaces 2019, 6.12: 1802058.
- Thin-film metal oxides in organic semiconductor devices: their electronic structures, work functions and interfaces, NPG Asia Materials 2013, 5.7: e55-e55.